Background) (1) Basic Concepts Overview - (1-1) Information Theory - Understanding Quantity of Information, ENTROPY, Information Gain, KL Divergence, and Cross-Entropy (Lecture: YouTube)
Topics Covered:
- Quantity of Information
- Entropy
- Information Gain
- KL Divergence
- Cross-Entropy
These topics are fundamental to understanding how information is processed and measured in machine learning and deep learning models. By studying and organizing these concepts, I aim to improve my understanding of the underlying principles and their applications in AI models.
- Quantity of information (정보량)
- 정보량 (놀람의 정도?) 은 사건의 확률과 관련이 있다.
- 확률이 높을수록 정보량은 낮으며 ex) 비행기가 하늘을 난다.
- 확률이 낮을수록 정보량은 높다. ex) 해가 서쪽에서 뜬다.
- 어떠한 정보를 수치화를 하고자 한다면.
- 첫번째 조건
- 확률 변수 (random variable) X
- X 의 정보량 h(X) 는 p(x) 에 대한 함수. 즉, h f(p)
- p(ease) = 0.999999
- p(west) = 0.000001
- h(west) > h(east) 여야 함
- p(x) 와 h(x) 는 monotonic 한 관계여야 한다. 즉 ,f 는 단조 감소 함수
- 두번째 조건
- 확률 변수(Random variable) X , Y
- X 는East, West 두가지값
- Y는Rain, Not Rain 두가지값
- X,Y 는독립
- 조건에 따른, 정보량 추측
- ENTROPY
- 주어진 데이터 집합의 혼잡도.
- 주어진 데이터 집합에서 서로 다른 종류의 레코드들이 섞여 있으면 엔드로피가 높고, 같은 종류의 레코드들이 섞여 있으면 엔트로피가 낮다.
- 0~1 사이의 값을 가지며, 가장 혼합도가 높은 상태의 값이 1 (분리가 안되어 혼합 되어 있는 것)이고, 반대는 0 (같은 데이터 결과만 존재, 혼합되어 있지 않은 것)이다. (하나의 레코드 만으로 구성된 값)
- Decision Algorithm 에서는 엔트로피가 높은 상태에서 낮은 상태가 되도록, 데이터를 특정 조건을 찾아 나무 모양으로 구분해 나간다. (다른 것에서 같은 것끼리.. 구분)
- 평균 적인 정보량을 계산.
- Minimize?
- 한 점에 확률이 다 몰려 있는 경우에는 0 이 된다.
- Information Gain
- 상위 노드의 엔트로피에서 하위노드의 엔트로피를 뺀값
- E(A) 는 A 라는 속성을 선택했을때 하위로 작은 m 개의 노드로 나누어 진다고 하면 하위 각 노드의 엔트로피를 계산한 후 노드의 속한 레코드의 개수를 가중치로 하여 엔트로피를 평균한 값
- 즉 , Gain(A)는 속성 A를 선택했을 때의 정보이득 양을 계산하는 수식으로 원래 노드의 엔트로피를 구하고
- 방금 구한 엔트로피를 선택한 후의 m개의 하위 노드로 나누어진 것에 대한 전체적인 엔트로피를 구한 후의 값을 뺀 결과이다.
- Gain(A) 값이 클수록 정보 이득이 큰 것이고, 변별력이 좋다는 것을 의미한다
- KL Divergence (Kullback-Leibler divergence )
- (위키피디아) 정의:
- 두 확률 분포의 "ENTROPY" 차이를 계산하는 데에 사용하는 함수
- 개념: 잘못된 모델링 (모델링 오류)로 인한 손해
- 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
- 상대 엔트로피(relative entropy), 정보 획득량(information gain), 인포메이션 다이버전스(information divergence) 라고도 한다.
- 특징
- 거리 개념이 아니다.
- 다만 거리 개념처럼 쓸 수 있는 방법이 존재합니다. 바로 Jensen-Shannon divergence 를 사용 하여, KL-divergence를 2가지를 구하고는 평균을 내는 방식을 사용 함
- Cross-Entropy
- Classification 할때 왜 Loss 함수는 Cross Entropy 일까?
- P(모분포, 정답)을 근사하기 위해 q(뉴럴넷)을 만들었음.
- H(p)는 q와 무관함, q의 parameter 로 미분하면 사라짐
- 그래서 H(p,q)를 loss 함수로 씀 - KL을 쓰는것과 마찬가지
- Mutual Information
- x 와 y 가 Independent 면 p(x,y) = p(x) * p(y)
- 만일 독립이 아니라면, KL divergence 를 이용하여 p(x) * p(y) 가 p(x,y) 에 얼마나 가까운지에 대한 idea 를 얻을 수 있다.
Reference
- https://eehoeskrap.tistory.com/13 [Enough is not enough]
- https://hyunw.kim/blog/2017/10/26/Cross_Entropy.html
- 팡요랩 (강의 슬라이드 : https://www.youtube.com/redirect?event=video_description&redir_token=QUFFLUhqa3ludEtTMFliaEU4eDNXbHMwaDExT3lEZi1Td3xBQ3Jtc0ttLXdMdjdkeXZKMXJUQUZBMVVUeG5QLVgySl9zUnB0ZWc0QjhTM0hoaE5mQUx1cTFqLWhrTlpSLXl2NzN0Mm54THFNd0ZuOTJMa0VVUE14OHh3NlBxek5YLXpUVDVvZ2hYTG1razhncGhmaGVTVkx2OA&q=https%3A%2F%2Fgithub.com%2Fminyoungjun%2FPang-yo%2Fraw%2Fmaster%2Fkldivergence.pdf )


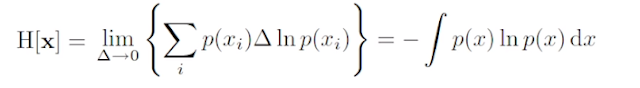




Comments
Post a Comment